
[2019年の豊島岡]
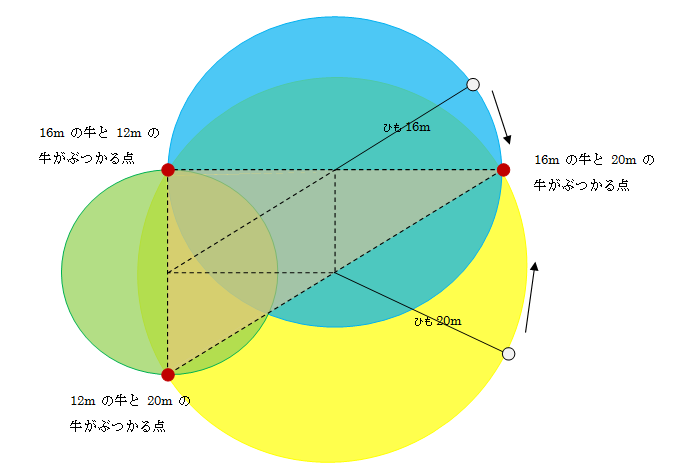
直角三角形ABCの3つの頂点の位置に牛が1頭ずつロープでつながれています。A、B、Cにつながれているロープの長さは、それぞれ16m、12m、20mです。
このとき、牛の動くことのできる部分の面積は全部で何m2ですか。牛の大きさやロープの太さは考えないものとします。
今年の1問をご紹介しました。前回の牛さん問題を思い出しながら、牛の動ける範囲を考えてみてください。

【答え】
1640m2
・半径12mの半円
・半径16mの半円
・半径20mの半円
・32mと24mの直角三角形(3:4:5)
計4つの面積の合計が1640m2
