<浅野中 平成20年>
図のような色のついた直角三角形があります。この三角形の各辺の中点を結び、真ん中にできた三角形の色を消したものが「1回目」の図です。同じようにしてできた三角形の色を消していきます。次の問いに答えなさい。
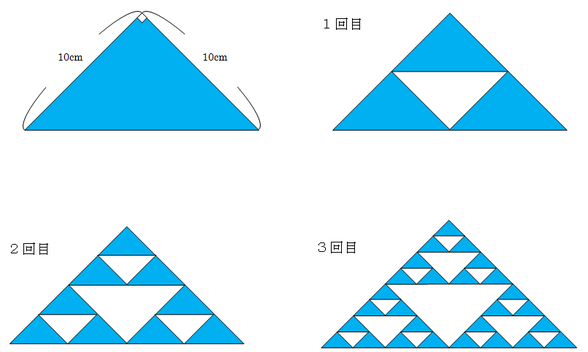
(1) 「5回目」の図で、色のついた三角形は何個ありますか。
(2) 「5回目」の図で、色のついた三角形1個分の面積を求めなさい。
<答え>
(1)243個 (3倍ずつふえていきます。1個⇒3個⇒9個⇒27⇒81個⇒243個)
(2)25 / 512(512分の25)
※解説 色のついた三角形の面積の大きさを考えていきます。
10×10÷2=50cm2(はじめの面積)
50÷4=12.5cm2(1回目の三角形ははじめの4等分です)
12.5÷4=3.125cm2(2回目の三角形はさらに1回目の4等分です)
以上のことから大きさが4分の1ずつになっていくことがわかります。
12.5÷4÷4÷4÷4= 25/512
